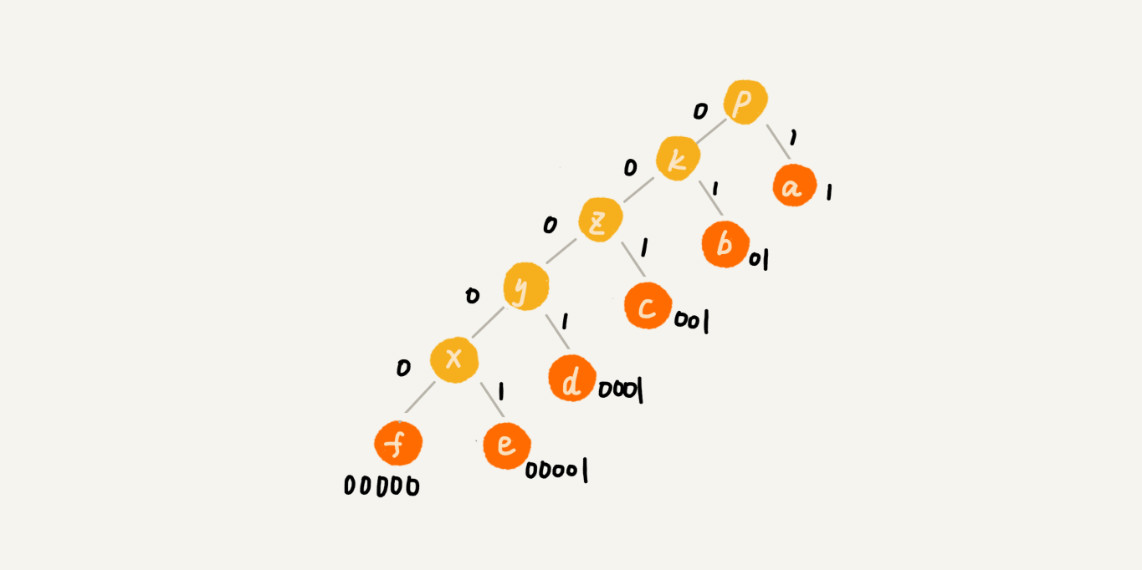
霍夫曼压缩编码考察了文本中有多少个不同字符,并考察每个字符出现的频率,根据频率的不同,选择不同长度的编码。
举例说明:
假设有一个包含1000个字符的文件,每个字符占1个byte(1byte=8bits),存储这1000个字符就一共需要8000bits,那有没有更加节省空间的存储方式呢?假设我们通过统计分析发现,这1000个字符中只包含6种不同字符,假设它们分别是a、b、c、d、e、f。而3个二进制位(bit)就可以表示8个不同的字符,所以,为了尽量减少存储空间,每个字符我们用3个二进制位来表示。那存储这1000个字符只需要3000bits就可以了,比原来的存储方式节省了很多空间。不过,还有没有更加节省空间的存储方式呢?
此时可以用霍夫曼编码。霍夫曼编码是一种十分有效的编码方法,广泛用于数据压缩中,其压缩率通常在20%~90%之间。霍夫曼编码不仅会考察文本中有多少个不同字符,还会考察每个字符出现的频率,根据频率的不同,选择不同长度的编码。霍夫曼编码试图用这种不等长的编码方法,来进一步增加压缩的效率。如何给不同频率的字符选择不同长度的编码呢?根据贪心的思想,我们可以把出现频率比较多的字符,用稍微短一些的编码;出现频率比较少的字符,用稍微长一些的编码。对于等长的编码来说,我们解压缩起来很简单。比如刚才那个例子中,我们用3个bit表示一个字符。在解压缩的时候,我们每次从文本中读取3位二进制码,然后翻译成对应的字符。但是,霍夫曼编码是不等长的,每次应该读取1位还是2位、3位等等来解压缩呢?这个问题就导致霍夫曼编码解压缩起来比较复杂。为了避免解压缩过程中的歧义,霍夫曼编码要求各个字符的编码之间,不会出现某个编码是另一个编码前缀的情况。
问题:如何根据频率的不同来进行编码呢?
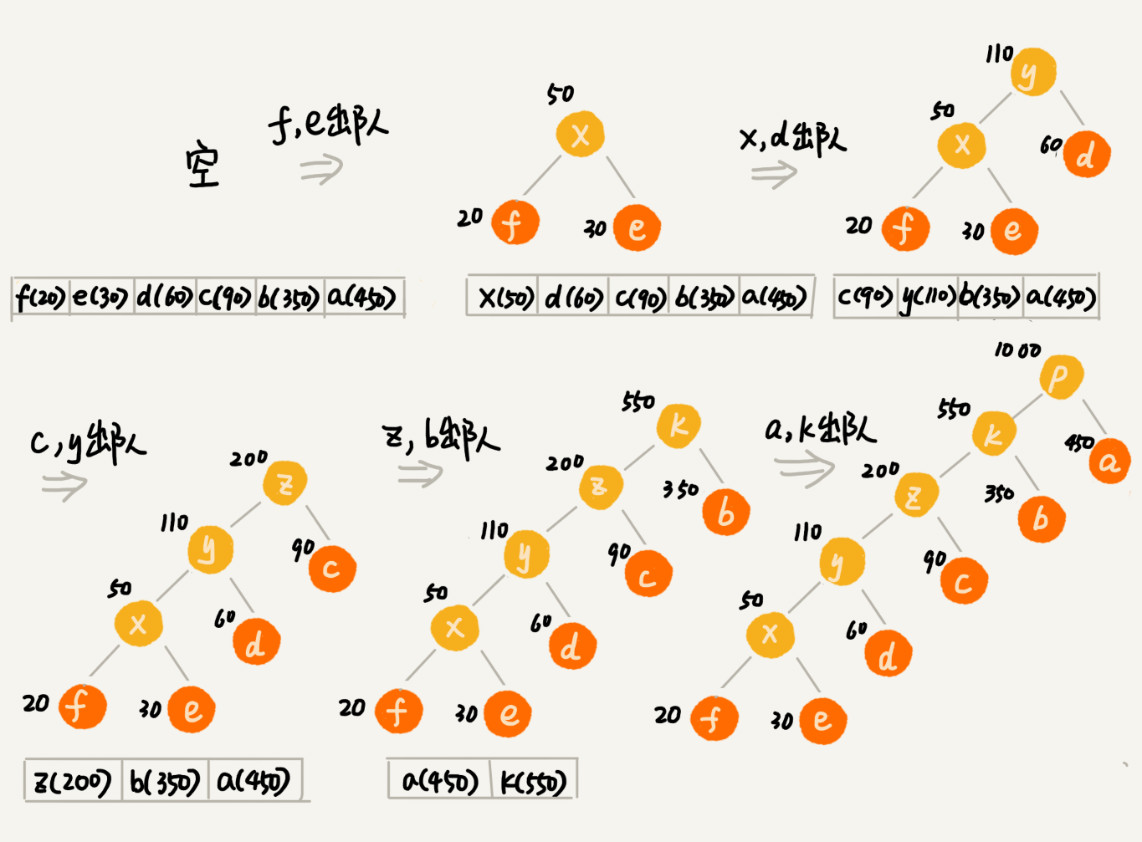
做法:把每一个字符看作一个节点,并且把其对应着的频率放在优先级队列中。
我们把每个字符看作一个节点,并且辅带着把频率放到优先级队列中。我们从队列中取出频率最小的两个节点A、B,然后新建一个节点C,把频率设置为两个节点的频率之和,并把这个新节点C作为节点A、B的父节点。最后再把C节点放入到优先级队列中。重复这个过程,直到队列中没有数据。
现在,我们给每一条边加上画一个权值,指向左子节点的边我们统统标记为0,指向右子节点的边,我们统统标记为1,那从根节点到叶节点的路径就是叶节点对应字符的霍夫曼编码。